Bipartite Matching Priblem
-> 두 가지 타입의 노드가 존재하는 그래프.
같은 타입의 노드 사이에는 엣지가 없다.
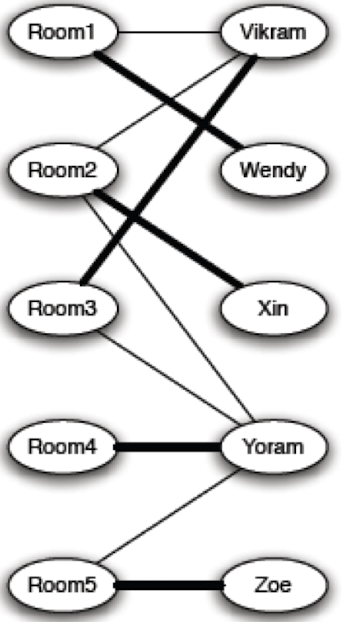
Perfect Matching & Constricted Set
위의 그래프에서 굵은 엣지는 perfect mathching이다.
각 타입별로 같은 수의 노드가 있는 그래프에서 perfect matching은
다음과 같은 방법으로 왼쪽 노드들을 오른쪽 노드에 할당 할 수 있는 경우이다.
(i) 각 노드들은 할당받은 노드와 엣지로 연결된다.
(ii) 두 개의 노드가 같은 오른쪽 노드에 할당되지 않는다.
오른쪽에 있는 모든 노드들은 왼쪽 노드를 할당받으면서, 두 개 이상의 왼쪽 노드를 할당받지 X
bipartite graph가 perfect matching일 때, 어떻게 perfec matching 상태를 쉽게 설명할 수 있을까?
-> edge들만 보이면됨! 위의 그림에서 굵은 엣지들
perfect mathcing이 없다는 건 어떻게 보일까? -- constricted set
constricted set
: 노드들의 집합을 S라고 할 때, N(S)을 S의 neighbor set이라고 하면,
만약 N(S)보다 S가 strictly larget -> S is constricted
Matching Theorem
: (좌우에 같은 개 수의 노드를 가지는) bipartite graph가 no perfect matching?
-> 그럼 반드시 constricted set을 포함함.
Valuations & Optimal Assignment
왼쪽 노드를 오른쪽 노드에 할당한다. 모든 (왼쪽 - 오른쪽 노드들)을 매칭시키기
어떻게?
오른쪽 노드들은 각각 왼쪽 노드들에 대한 valuations을 가지고 있음. 각자 어떤 왼쪽 노드가 더 좋은지 줄을 세워놓음.
그럼 각자가 좋아하는 노드를 할당해주는게 가장 좋은 매칭이겠지여
quality of an assignement = 각각의 오른쪽 노드들이 할당받은 노드들에 대해 가지는 valuation의 합!
optimal assignment: quality를 최대로 하는 assignment
-> 모두의 행복을 극대화
-> 모두에게 favorite item을 줄 필요는 없음.
Price & Market-Clearing Property
누가 매칭을 시켜주나? - 중앙관리자가?
central coordination
: 중앙 관리자가 perfect matching or optimal assignment를 결정해 줌
decentralize the market
근데 우리는 이 중앙 관리자가 없는 경우를 볼 거
- 그럼 매칭 어떻게 결정?? -> 특별한 전략에 의해서 매칭이 결정됨!
개인들은 본인들의 valuation, price에 따라 자신의 이익을 따라가며 매칭이 결정됨.
노드들을 seller와 buyer로 생각해 보자.
seller는 왼쪽 노드, buyer는 오른쪽 노드
seller i는 본인의 item에 대해 price pi를 결정함. (pi >= 0)
가격은 누가 사든 똑같다.
buyer들은 각 seller에 대해 valuations를 가지게 됨.
buyer j는 seller i의 아이템에 대해 valution vij를 가짐.
만약 buyer j가 seller i의 아이템을 가격 pi에 산다면,
buyer j의 payoff = pi - vij
사지 않았을 때는 0
buyer j가 자신의 이득을 극대화하려면 -> pi - vij를 극대화해야 함
preferred sellers of buyer j
= buyer j의 payoff를 극대화하는 seller!
Market-Clearing Prices (MCP)
모든 buyer들은 자신의 payofff를 극대화하는 item을 선택함.
payoff를 음수로 만드는 경우 선택하지 않음.
모든 buyer들이 자신의 payoff를 극대화하는 item을 선택한 결과,
각기 다른 item들을 assignment (perfect matching)이라면 이때의 가격이 market-clearing prices!

이 경우는 market clearing prices.
x는 a, y는 c, z는 b와 매칭이 됨.
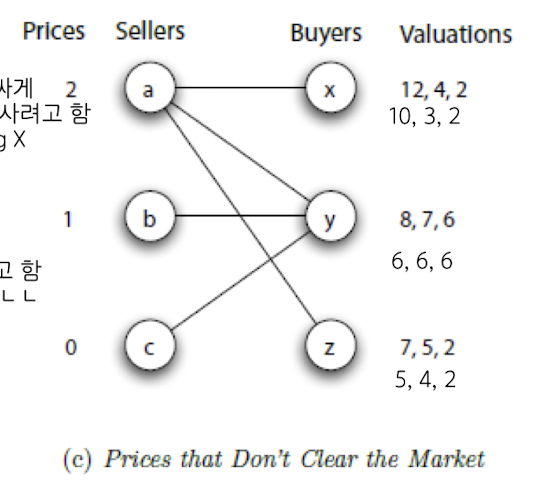
이 경우는 x - a, z - a 둘 다 같은 item을 선택하기 때문에 market clearing price X
Buyer들이 가지는 valuation은 고정.
price가 변하면서 각자의 payoff (price - valuation)이 변하게 된다.
-> 그 결과 perfect matching이 생기면 그 가격이 결정
Preferred-seller graph
위에 그려진 그래프.
각 buyer들이 선호하는 seller들을 edge로 연결해 놓은 그래프.
Market-clearing prices (MCP)
- preferred-seller graph의 결과가 perfect matching일 때의 가격 집합
- 바이어들 사이의 논쟁(서로 같은 걸 두고 싸움?)을 해결함 - 모두 다른 아이템을 선택할 때 각자의 payoff가 최대가 최면서
MCP 특성
- Existence of MCP
- 어떤 buyer valuations 집합에 대해서도, MCP가 존재한다.
- Optimality of MCP
- 어떤 MCP 집합에 대해서도, 결과로 나오는 preferred-seller graph의 total valution이 최대가 됨
- MCP 집합과 최종적인 perfect matching은 전체 바이어, 셀러에 대해 가능한 payoff의 최댓값임
oprimality of MCP ?
payoff가 최대가 되는 건 알겠는데 왜 valuation도 최대가 된다는 건지 잘 안 와닿음.
M: perferred-seller graph에서 perfect matching이라고 하자.
M의 total payoff는
- 각각의 바이어들을 본인의 payoff를 극대화하는 아이템을 선택함
-> 전체 payoff의 합도 최대가 됨
- payoff = valutaion - price
- total payoff of M = total valution of M - sum of all price
-> 여기서 sum of all price는 M이랑 독립적임. price가 바뀌면서 M이 결정되는 것이기 때문에, M 자체가 가격에 영향을 주지 않음. M이 찾아지면 가격은 변하지 않고 그 값으로 결정되는 것임. 가격은 이미 결정된 값으로, 즉 상수 취급함.
-> 그럼 저 식에서 payoff가 최대하는 건 (total valuation - total price) 또한 최대라는 뜻인데, 여기서 뒤에 -total price는 상수이기 때문에, 결국 total valuation도 최대가 됨 !
Construction MCP
MCP가 뭔지, 어떤 특징을 가지는지 알겠는데
특정 buyer valiations에 대해 어떻게 MCP를 찾아낼까 ?
- 전에 봤던 auction 방법을 적용함
perfect matching이 아닌 상태에서 -> perfect matching으로 가야 함.
perfect mathcing이 아니라는 것은 constricted set이 존재한다는 것이고
constrincted set S > neighbors set N(S)라는 것
-> 아이템의 개수보다 해당 아이템을 가지고 싶은 사람들이 더 많음
-> 해결 불가 -> 가격을 올리자
constricted set S: 해당 아이템을 사고 싶어 몰린 바이어들
neighbors set N(S): 바이어들이 몰린 아이템
ascending auction 처럼 가격을 점점 올려가면서 MCP를 찾자 !
1. 처음에 모든 가격을 0으로 초기화함
2. preferred-seller graph 그리기
3. 바이어들이 react - payoff 극대화하는 아이템 선택
4. if perfect matching ? -> end
5. else -> 가격 조정함
-> 다시 3번으로
처음에 0으로 셋팅해서 최종적으로 가장 낮은 아이템의 가격은 0이 됨.
만약 이거보다 큰 p 라면 전부 p 씩 빼주면 됨.
가격 조정은 어떤 식으로 ?
- 바이어들이 몰린 over-demanded sellers N(S)들의 가격을 한 번에 올려줌
그리고 MCP는 꼭 한 가지만 있는 거 아님! 가격 조정 과정에 따라 여러 가지 존재 가능
또한, 위의 과정대로 하면 결국에는 MCP를 반드시 찾고 끝남
'Computer Science > Software Application' 카테고리의 다른 글
| [소프트웨어 응용] Sponsored Search Markets (1) | 2023.12.18 |
|---|---|
| [소프트웨어 응용] Auctions (3) | 2023.12.17 |
| [소프트웨어 응용] Network Community & Community Detection (0) | 2023.10.20 |
| [소프트웨어 응용] Structural Holes (0) | 2023.10.20 |
| [소프트웨어 응용] 네트워크의 커뮤니티 구조 (1) | 2023.10.20 |